Предлагаю вашему вниманию скромную презентацию, по которой я с горем пополам выступил год назад на конференции про интернет-магазины.
И хоть она и называется «Дизайн и юзабилити интернет-магазина», но про конкретно интернет-магазины там ничего нет. В ней вообще про дизайн, юзабилити и вот это всё.
Автор: Крис Пирсон (CHRIS PEARSON), декабрь 2011
Оригинал: http://www.pearsonified.com/2011/12/golden-ratio-typography.php
Перевод: Егор Стремоусов (28 декабря 2011)
Прямо сейчас эта математическая симфония звучит на вашем сайте. Каждый его посетитель подсознательно чувствует ее и, что более важно, предрасположен реагировать на нее определенным образом.
В связи с чем возникает главный вопрос: эта симфония приятна и притягательна, или же она действует отталкивающе и лишь усложняет коммуникации с вашими читателями?
Как известно, эта симфония не прерогатива веба. Вы «слышите» ее каждый раз когда читаете книгу, газету, журнал или сайт — что угодно, что содержит типографику.
На первый взгляд вам может показаться, что математика и типографика не имеют ничего общего между собой. Ведь, в конце концов, типографика состоит из букв и слов, а математика…ну…из чисел.
Но на самом деле типографика — это комбинация художественных форм символов и математических пропорций, изысканный брак между формой и функцией.
Когда математические пропорции типографики находятся в гармонии, ваш сайт (а точнее содержание вашего сайта) выглядит привлекательно для посетителей.
И наоборот, когда пропорции несбалансированы, то содержание уже не так притягательно для его читателей, а сам сайт выглядит хаотично и безалаберно.
Вывод из этого:
Математические пропорции типографики — это жизненно важный фактор для восприятия сайта и его содержания.
Каким же образом можно настроить пропорции, чтобы получалась красивая математическая симфония? Давайте совершим путешествие в типографическую кроличью нору и узнаем ответ на этот вопрос!
Каждый параграф текста, который вы видите, имеет 3 основных измеряемых параметра. Первые два, размер шрифта и высота строки — измеряются по вертикали.
Размер шрифта — это расстояние от верней точки заглавной буквы (S) до нижней границы нижних выносных элементов (y). Высота строки делится пополам и равномерно распределяется сверху и снизу от центра строки.
Третий параметр, длина строки, измеряется по горизонтали.
Эти три параметра вместе определяют то, как вы воспринимаете текст.
Для того, чтобы понять, как эти параметры взаимодействуют, полезно рассмотреть несколько примеров, в которых одна из метрик изменяется, а другие остаются постоянными. Кроме того, такой способ позволяет увидеть, как каждый из параметров влияет на два других.
Ниже, на рисунке 3, высота и длина строки зафиксированы, а размер шрифта изменяется от 13 до 16 пикселей.
На рисунке 3, в первом абзаце высота строки достаточно велика по отношению к размеру шрифта, что создает щедрые междустрочные пробелы, а во втором абзаце — наоборот: высота строки слишком мала для нормальных просветов между строк. Это дает ощущение некой зажатости текста.
Отсюда можно сделать важный вывод: если размер шрифта увеличивается, то и высота строки должна увеличиваться, чтобы сохранить геометрические пропорции текста. Другими словами:
Размер шрифта и высота строки имеют прямо пропорциональную зависимость.
В следующем примере размер шрифта и высота строки фиксированные, а длина строки варьируется от 233 до 466 пикселей.
Несмотря на тот факт, что на рисунке 4 высота строки одинакова в обоих абзацах, их удобочитаемость значительно отличается из-за разной длины строк.
Чем больше длина строк, тем сложнее скользить взглядом между ними (движение глаз от конца одной строки к началу следующей), при условии, что высота строки не увеличивается соответственно.
Эти выводы подтверждают проведенные исследования. В 2004 году Мэри Дайсон (MARY C. DAYSON) из Института Чтения (какая ирония, да?) установила, что:
«Большая длина строки говорит о необходимости такого междустрочного пространства, который бы позволил глазам безошибочно находить следующую строку при возвратном скольжении взгляда…»
Что это значит для нас? Это означает, что высота и длина строки имеют определенную математическую зависимость, а конкретно:
Для любого размера шрифта высота строки должна увеличиваться, если увеличивается ее длина.
Но каков математический смысл этого соотношения?
Ответ на этот вопрос проще, чем может показаться на первый взгляд. Дело в том, что природа дала нам правило для создания красивых и эффективных пропорций.
Подмеченное во флоре и фауне, в формах галактик и даже в ДНК, это правило настолько распространено вокруг, что люди заметили его уже тысячелетия назад. Результаты его применения можно проследить на протяжении всей истории искусства и архитектуры.
Что же это за удивительные пропорции, которые «склеивают осколки этого мира»?
Конечно же, я говорю о золотом сечении.
Когда природе нужны пропорции, чтобы соотнести вещи и навести порядок в любом масштабе, она стремится использовать золотое сечение.
В случае типографики целью является соотнесение размера шрифта, высоты и длины строки эстетически приятным и упорядоченным способом.
Так, может быть, золотое сечение применимо для решения этой задачи?
Как вы уже, наверное, догадались, ответом является решительное «да»! И вот как это работает.
Во-первых, размер шрифта (f) и высота строки (l) соотносятся через коэффициент подобия (h). Базовое математическое уравнение выглядит следующим образом:
Согласно этому уравнению, оптимальная высота строки получится в том случае, если коэффициент подобия h будет равен золотому сечению φ. Это дает нам следующее уравнение:
К сожалению, знания оптимальной высоты строки для заданного размера шрифта недостаточно.
Ранее мы рассмотрели, как каждый из 3 типографских параметров (размер шрифта, высота и длина строки) влияет на два других. Поэтому, нельзя говорить о высоте строки или размере шрифта без учета длины строки.
Из этого следует, что должна существовать оптимальная длина строки, соответствующая оптимальной высоте строки из уравнения выше.
Проблема заключается в том, что не известно, в каком именно соотношении находятся высота и длина строки. Все, что известно, так это то, что длина строки должна быть существенно больше ее высоты.
Используя простейшие математические модели, можно сделать обоснованное предположение, что зависимость между высотой и длиной строки носит экспоненциальный характер. Вот простое уравнение, иллюстрирующее данное утверждение:
Эти уравнения примечательны тем, что впервые подводят под параметры текста прочную математическую основу.
На заметку дизайнеру: Золотое сечение типографики призвано служить основой для правильного типографского набора. Такие факторы, как x-высота символа и другие параметры шрифта, тоже влияют на типографику и должны учитываться в конечном дизайнерском решении. Однако, золотое сечение типографики обеспечивает наиболее рациональную стартовую точку для работы в этом направлении.
Однако, тут есть небольшая проблема: веб не настолько точен, как эти уравнения.
Известно, что веб-дизайнеры вынуждены использовать целочисленные значения для таких вещей, как размер шрифта, высота и длина строки (и так будет до тех пор, пока субпиксельный рендеринг не станет реальностью).
Приведенные уравнения дают на выходе большую точность и множество знаков после десятичной запятой, простое округление которых до ближайшего целого приводит к существенным ошибкам, нарушающим в итоге точность типографских пропорций.
Суть в том, что веб дискретен, и, следовательно, представленные выше идеальные уравнения в реальности не пригодны для тонкой настройки параметров типографики.
Получается, что если вы хотите использовать золотое сечение типографики на своем сайте, то вам понадобится корректировка результатов этих уравнений.
Чтобы понять, как выпоняется корректировка, давайте рассмотрим пример.
Для шрифта с размером 16 пикселей идеальная высота строки получается тогда, когда коэффициент h равен золотому сечению (≈1.61 — Прим. переводчика). Это дает оптимальное значение для высоты строки, равное 25.88854 пикселя. Используя это значение, вы можете вычислить, что соответствующее оптимальное значение для длины строки равно 670.21670 пикселя.
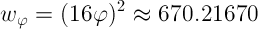
Если вы попробуете использовать эти значения в вашем CSS-коде, то столкнетесь с рядом проблем.
Поскольку разрешены только целочисленные значения, веб не сможет отобразит высоту строки, равную 25.88854 пикселя. В лучшем случае высота строки станет равна 26 пикселям.
Но 26 пикселей — это больше, чем оптимальная высота строки, полученная из уравнения. А как мы уже знаем, нельзя изменять высоту строки (даже на чуть-чуть!) без изменения соответствующей длины строки (в противном случае конечные пропорции не будут «золотыми»).
Поэтому операция округления высоты строки с 25.88854 до 26 пикселей требует, чтобы конечная длина строки должна быть больше, чем 670.21670 пикселя.
Эту суть корректировки параметров типографики:
Если длина вашей строки меньше, чем оптимальная длина, то соответствующая высота строки должна быть меньше, чем получается по золотому сечению. И наоборот, если длина строки больше оптимальной, то и высота строки тоже должна быть больше расчетной.
Ниже приведен рисунок, который иллюстрирует эту концепцию для самых используемых размеров шрифта.
С точки зрения математики, скорректированные уравнения более сложные, чем уравнения, которые мы видели до этого. Но к счастью для вас, я уже провел тяжелую работу по их получению, поэтому вы можете сконцентрироваться на концепции и ее результатах.
В итоге вам нужны 2 скорректированных уравнения для разных случаев, с которыми вы столкнетесь при параметризации типографики. В зависимости от ситуации, вам понадобится определить
скорректированную высоту строки, зная размер шрифта и длину строки;
или скорректированную длину строки, зная размер шрифта и высоту строки.
Вычисления проводим при помощи следующих уравнений:
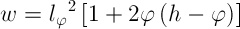
Используя второе уравнение, можно определить скорректированную длину строки для рассмотренного выше примера с размером шрифта в 16 пикселей и целочисленной высотой строки в 26 пикселей.
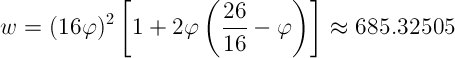
Скорректированная длина, которая поддерживает золотые типографские пропорции, в этом случае будет равна 685.32505 пикселя. Для использования этого значения в вебе, оно должно быть округлено до 658 пикселей.
А теперь давайте рассмотрим другой, более насущный пример, который покажет как вы можете подправить типографику на вашем сайте прямо сейчас:
Что, если вы захотите использовать шрифт в 16 пикселей для текста шириной 550 пикселей?
Какой должна быть высота строки в этом случае?
Вы можете решить эту задачу следующим образом:
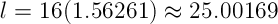
Полученное значение равно 25.00169 пикселя. Опять же, для использования в вебе это значение должно быть округлено до ближайшего целого. Значение скорректированной высоты строки равно 25 пикселям.
Очевидно, что расчеты большого числа математических формул при работе с типографикой сайта могут быстро утомить.
Специально для решения этой проблемы я разработал калькулятор золотого сечения типографики, который позволяет невероятно легко определить ее параметры для любой ситуации!
Умный и гибкий калькулятор даст вам золотые типографские рекомендации, основанные на ваших исходных данных.
Если вы укажите размер шрифта, то калькулятор рассчитает для него оптимальную высоту и длину строки.
Если вы введете длину строки, то калькулятор покажет вам для нее по два наилучших размера шрифта и два соответствующих значения высоты строки.
Если вы укажите и размер шрифта, и длину строки, то получите целый набор:
Оптимизированные параметры типографики для вашего размера шрифта и длины строки.
Лучшие значения параметров типографики для длины строки, которую вы указали.
Дополнительные варианты значений параметров типографики для длины строки, которую вы указали.
Оптимальные значения типографики для указанного размера шрифта.
Попробуйте поиграть с калькулятором золотого сечения и познайте невиданное качество типографики!
Я уже намекал на это, но теперь заявляю открыто: вещи, которыми я поделился с вами выше, не ограничиваются применением в вебе. На самом деле…
Золотое сечение типографики можно использовать для любого текста в любой среде.
Книги, газеты, журналы, веб-сайты, электронные издания, все что захотите. Везде можно извлечь выгоду из улучшенных пропорций этого сечения.
Теперь, когда вы начали смотреть на мир сквозь призму золотого сечения, вы увидите несчетное количество возможностей оптимизации для типографики.
Золотые пропорции проявляются по всей вселенной в тех местах, где форма и функция объединяются для создания прекрасного, эффективного и полезного результата.
Запомнили математическую симфонию типографики?
Благодаря золотому сечению типографики вы можете быть уверены, что на вашем сайте для каждого посетителя звучит золотая симфония.
Ритм в теории музыки — соотношения длительностей
звуков (нот) в их последовательности.
— Википедия
В вебе вертикальный ритм можно охарактеризовать соотношениями вертикальных размеров визуальных элементов и отступов между ними.
Верстка вертикального ритма — это, в первую очередь, правильная расстановка текста, изображений и других элементов по базовой сетке.
Для точного попадания в базовую сетку важно соблюдать высоту линейного блока, который образуется из последовательности одного или более строчных блоков.
В общем случае, строчный блок — это прямоугольник с минимально возможными размерами, в который можно вписать элемент.
В свою очередь, линейный блок — это прямоугольник с минимально возможными размерами, в который можно вписать все строчные блоки, расположенные на одной линии в рамках единого контекста форматирования.
При форматировании и отрисовке страницы, браузер рассчитывает размеры строчного блока для каждого элемента, исходя из совокупности его CSS-свойств.
Расчет интересующей нас высоты линейного блока происходит по следующему алгоритму:
Определяется высота каждого строчного блока в линейном блоке.
В соответствии со свойством vertical-align строчные блоки выстраиваются по вертикали.
Следует помнить, что пустые строчные блоки так же влияют на расчет высоты линейного блока, поскольку, несмотря на отсутствие содержимого, имеют внутренние и внешние отступы (padding и margin), границу (border), высоту строки (line-height), а также заданные размеры (width и height).
Таким образом, значимыми CSS-свойствами для расчета высоты линейного блока являются:
padding-top, padding-bottom
margin-top, margin-bottom
border-top, border-bottom
height
font-size
line-height
Рассмотрим, как каждое из этих свойств влияет на высоту и позиционирование строчного блока, и, как следствие, косвенно влияет на высоту линейного блока.
Свойства padding-top, padding-bottom, margin-top, margin-bottom, border-top и border-bottom не увеличивают высоту строчного блока на собственное значение, однако учитываются при расчете высоты линейного блока.
Жестко заданное значение свойства height задает фиксированную высоту строчного блока. При этом стоит учитывать то факт, что высота блока не изменится даже в том случае, когда содержимое не помещается в указанные пределы.
При прочих отсутствующих значениях, высота строчного блока равна значению line-height. Свойство font-size напрямую не влияет на расчет высоты строчного блока, но может делать это косвенно в ситуации, когда значение line-height задается относительным.
Важно понимать, что свойства line-height и font-size связаны между собой понятием интерлиньяжа.
В CSS, интерлиньяж — это разница между размером шрифта и вычисляемым значением line-height. Эта разница в виде свободного пространства распределяется сверху и снизу от отображаемых глифов поровну (дробные значения округляются до целых). Образованные части называются половинным интерлиньяжем.
Если значение line-height меньше, чем значение font-size, то образуется отрицательный интерлиньяж, что может приводить к наложению текста в соседних линейных блоках друг на друга.
Свойство vertical-align смещает строчные блоки внутри линейного блока по вертикали, «растягивая» его высоту
Обратите внимание, что реализация вертикального позиционирования блоков в различных браузерах отличается при условии, что размер содержимого блока больше его габаритов.
При верстке вертикального ритма хорошим тоном считается использование техники reset css, которая помогает убрать нежелательное влияние стилей, заданных в браузерах по-умолчанию. Это, в свою очередь, влечет за собой необходимость разработчику самостоятельно задавать значения для свойств, относящихся к размеру шрифта и отступам.
Для решения этой задачи можно воспользоваться специальным генератором стилей. Однако, при дальнейшем использовании этих стилей могут возникнуть проблемы с заданием необходимой высоты линейного блока, поскольку они, как правило, не универсальны и требуют доработки в контексте решаемой задачи.
Рассмотрим ситуацию, когда на одной строке находятся два текстовых элемента с разными размерами шрифта. Стили сброшены, а вертикальное выравнивание элементов осуществляется по базовой линии.
Для определения требуемых стилевых правил воспользуемся упомянутым выше (или любым другим) генератором вертикального ритма.
В этом случае мы получим нежелательное увеличение высоты линейного блока, которое в дальнейшем даст сбой в ритме для нижеследующих элементов.
Причина проблемы в выравнивании по базовой линии (навязано набором правил из reset css) и фиксированном line-height (определен генератором). Уменьшение размера шрифта ведет к увеличению половинного интерлиньяжа и к смещению второго строчного блока вниз, что, в свою очередь, приводит к увеличению высоты линейного блока.
Для решения проблемы можно переопределить значение line-height для второго элемента, согласовав его с нижней границей первого блока.
Генераторы вертикального ритма:
http://topfunky.com/baseline-rhythm-calculator/
http://drewish.com/tools/vertical-rhythm
http://toki-woki.net/p/Boks/
http://baselinecss.com/
Рекомендуемые к прочтению статьи о верстке вертикального ритма:
http://www.alistapart.com/articles/settingtypeontheweb
http://webtypography.net/Rhythm_and_Proportion/Vertical_Motion/2.2.1/
http://24ways.org/2006/compose-to-a-vertical-rhythm
http://thegrids.ru/literature/31
http://habrahabr.ru/blogs/typography/78322/
PEREDELKA 